You can use our interactive quantum circuit simulator to run simple quantum programs on our servers which simulate a quantum computer (no account required!). If you are not familiar with quantum computing, have a look at our tutorials.
How to use the quantum circuit simulator?
We are assume that you are familiar with the basics of quantum mechanics and quantum algorithms & quantum circuits.
A quantum circuit simulator is a tool that allows you to construct and simulate simple quantum circuits graphically, i.e., without actually writing code. Every primitive gate $\{X,Y,Z,H,\dots\}$ is represented by a unique symbol that covers one, two, or three qubits, depending on the gate. The symbols can be dragged with the mouse and dropped onto the quantum circuit to construct a quantum algorithm. Our quantum circuit simulator then translates this graphical representation into an equivalent textual representation, a programming language known as OpenQASM. This code is sent to and run by our servers that simulate a quantum computer. The measurement results are then sent back to your browser and displayed by the quantum circuit simulator.
Our quantum circuit simulator is an interactive web application to write and simulate simple quantum algorithms without having to sign up for an account. It can be embedded into webpages like above.
Beware:
The quantum circuit representation is only useful for simple quantum algorithms (with few qubits and gates). However, it can be very helpful to illustrate the operation of a quantum computer and to develop new algorithms. To implement “real” algorithms on hundreds or thousands of qubits, one would write OpenQASM code directly.
Here we describe how our quantum circuit simulator works step by step:
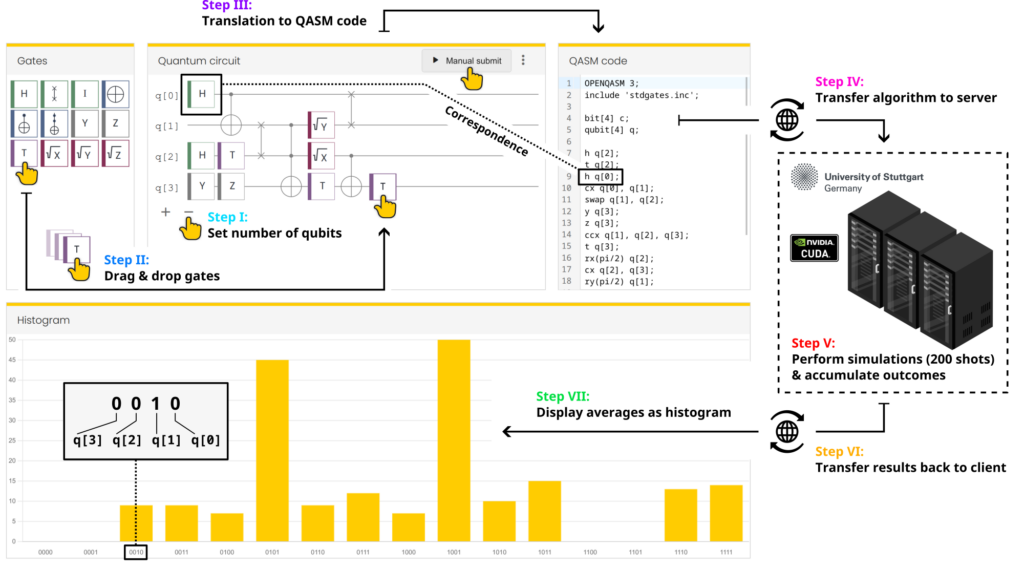
Step I
Use the + and - buttons in the Quantum circuit box to set the number of qubits (1–10 qubits are possible). The qubits are labeled as q[i] with index i=0,1,...,N-1 for N qubits (in informatics, indices typically start from 0 and not 1).
Step II
Use your mouse to drag quantum gates from the Gates box into the Quantum circuit box. Drop the gate on the horizontal line that corresponds to the qubit that the gate should be applied to. You can insert gates before other gates by “squeezing” them in gaps between gates. To delete gates, grab them and pull them out of the quantum circuit.
Step III
Whenever you change the quantum circuit, the quantum circuit simulator automatically translates the circuit into an equivalent OpenQASM code representation (shown in the QASM code box).
Step IV
After the OpenQASM code has been updated, it is automatically sent to our QRydDemo API at the University of Stuttgart and queued in the job list of our classical simulator. You can also manually submit a new job by clicking the Manual submit button. This is useful to observe the statistical fluctuations of the measurement outcomes.
Step V
Our simulator of a quantum computer executes your quantum circuit 200 times and accumulates the measurement outcomes. The simulator runs on dedicated graphics cards to accelerate the computations. When our quantum computer is up and running, this simulation can be replaced by a quantum computation on a real quantum computer.
Note: To simulate quantum algorithms on up to 10 qubits, it is not necessary to use dedicated hardware like graphics cards. These simulations could be performed by your local computer (even in your browser). However, we use this simulation pipeline & hardware also productively to simulate up to 32 qubits and optimize our gate protocols. It was then straightforward to connect the quantum circuit simulator to this pipeline, so that you automatically profit from improvements of our simulators.
Step VI
The accumulated measurement results are sent back to the quantum circuit simulator in your browser.
Step VII
The results are displayed in the Histogram box of the quantum circuit simulator. The y-axis shows the number of shots that resulted in a specific qubit configuration after measurement (all bars therefore add up to 200). On the x-axis the $2^N$ possible measurement outcomes are shown (for $N$ qubits). For example, the label 0010=q[3]q[2]q[1]q[0] corresponds to the measured state $\ket{q_3q_2q_1q_0}=\ket{0010}$.
Gates
Here we list and define all primitive gates that are currently supported by the quantum circuit simulator. Gates marked as “native” are directly supported by the QRydDemo quantum computing platform. Gates that are not native are automatically translated into native gates when the quantum algorithm is compiled on our servers.
Note: The native two-qubit gate of the QRydDemo platform is a Controlled-Phase gate which is currently not directly available in the quantum circuit simulator (it will be in an upcoming version). The multi-qubit gates that are available are automatically translated into Controlled-Phase gates by our compiler.
| Name | Symbol | # Qubits | Definition | Native? |
|---|---|---|---|---|
| Identity | 1 | $I=\begin{pmatrix}1&0\\0&1\end{pmatrix}$ | Yes | |
| Pauli-X |  | 1 | $X=\begin{pmatrix}0&1\\1&0\end{pmatrix}$ | Yes |
| Pauli-Y |  | 1 | $Y=\begin{pmatrix}0&-i\\i&0\end{pmatrix}$ | Yes |
| Pauli-Z |  | 1 | $Z=\begin{pmatrix}1&0\\0&-1\end{pmatrix}$ | Yes |
| Sqrt-X | 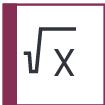 | 1 | $\sqrt{-iX}=\frac{1}{\sqrt{2}}\begin{pmatrix}1&-i\\-i&1\end{pmatrix}$ | Yes |
| Sqrt-Y | 1 | $\sqrt{-iY}=\frac{1}{\sqrt{2}}\begin{pmatrix}1&-1\\1&1\end{pmatrix}$ | Yes | |
| Sqrt-Z (Phase) |  | 1 | $S=\sqrt{Z}=\begin{pmatrix}1&0\\0&i\end{pmatrix}$ | Yes |
| $\pi/8$ (T) |  | 1 | $T=\begin{pmatrix}1&0\\0&e^{i\pi/4}\end{pmatrix}$ | Yes |
| Hadamard |  | 1 | $H=\frac{1}{\sqrt{2}}\begin{pmatrix}1&1\\1&-1\end{pmatrix}$ | No |
| Controlled-NOT (CNOT) |  | 2 | $\mathrm{CNOT}=\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{pmatrix}$ | No |
| Swap | 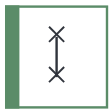 | 2 | $\mathrm{SWAP}=\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\end{pmatrix}$ | No |
| Toffoli (CCNOT) | 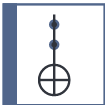 | 3 | $\mathrm{Toff}=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \end{pmatrix}$ | No |