
The phenomenon of entanglement is perhaps the most prominent feature of quantum mechanics. In this tutorial you can learn how this can be done with the quantum circuit simulator and how entanglement is reflected in the measurement outcomes.
Prerequisite Tutorials:
• The Basics of Quantum Mechanics
• Quantum Algorithms & Quantum Circuits
• Superpositions, Randomness & Interference
Open the quantum circuit simulator in a separate window
The phenomenon of entanglement is perhaps the most prominent feature of quantum mechanics. As it happens, it is also crucial for quantum computers to outperform their classical counterparts. Therefore it is not uncommon for larger quantum algorithms to start off with the preparation of entangled pairs (or even groups) of qubits. Here you will learn how this can be done with the quantum circuit simulator and how entanglement is reflected in the measurement outcomes.
Creating an entangled pair of qubits
Use the + and - buttons in the Quantum Circuit box to setup the circuit simulator with two qubits q[0] and q[1].
To generate entanglement between two qubits we need two gates: The Hadamard gate $H$ (which operates on a single qubit), and the Controlled-NOT gate $\mathrm{CNOT}$ (which operates on a pair of qubits). The Hadamard gate has been discussed above in “Superpositions, Randomness, and Interference”. The Controlled-NOT gate flips one qubit (the target) depending on the state of another qubit (the control). Its action on quantum states is defined by its action on the four basis states of two qubits:
$$
\begin{aligned}
\ket{00}\;&\xrightarrow{\;\mathrm{CNOT}\;}\;\ket{00}\\
\ket{01}\;&\xrightarrow{\;\mathrm{CNOT}\;}\;\ket{01}\\
\ket{10}\;&\xrightarrow{\;\mathrm{CNOT}\;}\;\ket{11}\\
\ket{11}\;&\xrightarrow{\;\mathrm{CNOT}\;}\;\ket{10}
\end{aligned}
$$Note how the state of the second (target) qubit is flipped if and only if the state of the first qubit (control) is $\ket{1}$. In the circuit simulator, the Controlled-NOT gate is depicted by a box with $\bullet$ and $\oplus$ connected by a line. The $\bullet$ signifies the control qubit, the $\oplus$ represents the target qubit.
To generate an entangled state, we first create a superposition state on the qubit q[0], and then use this qubit as the control of a Controlled-NOT gate with q[1] as the target. To do this, drop a Hadamard gate and a Controlled-NOT gate in the circuit simulator as follows:
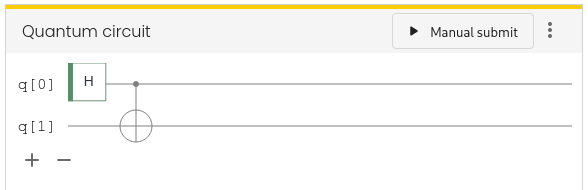
Run this quantum circuit on the quantum simulator multiple times and observe the measurement outcomes. Can you theoretically explain the histogram? Can you explain with these results why entanglement cannot be used to send information faster than light?
Explanation
The two gates transform the initial state as follows:
$$
\begin{aligned}
\ket{\Psi_\mathrm{initial}}=\ket{00}
&\;\xrightarrow{\; H_0 \;}\;
\frac{1}{\sqrt{2}}\ket{00}+\frac{1}{\sqrt{2}}\ket{10}
\\
&\;\xrightarrow{\; \mathrm{CNOT}_{0,1} \;}\;
\frac{1}{\sqrt{2}}\ket{00}+\frac{1}{\sqrt{2}}\ket{11}
=\ket{\Psi_\mathrm{final}}
\\
&\;\xrightarrow{\mathrm{Measure}}\;
\begin{cases}
\ket{00}&:\,p_0=0.5\\
\ket{01}&:\,p_1=0\\
\ket{10}&:\,p_2=0\\
\ket{11}&:\,p_3=0.5
\end{cases}
\end{aligned}
$$Here $H_0$ denotes a Hadamard gate applied to the qubit with index 0 and $\mathrm{CNOT}_{0,1}$ is a Controlled-NOT gate with control qubit 0 and target qubit 1. As a final result, one measures the states $\ket{00}$ and $\ket{11}$ with a probability $p_0=p_3=0.5$ each. The states $\ket{01}$ and $\ket{10}$ are never observed.
The state $\ket{\Psi_\mathrm{final}}=1/\sqrt{2}\left(\ket{00}+\ket{11}\right)$ is said to be entangled because on measuring the two qubits, it turns out that, while the outcome of one of them seems random, its partner always happens to choose the same value. This remains true even if the two qubits are separated by large distances after the Controlled-NOT gate has been applied: If you look at one of the two qubits, it randomly decides to collapse into the state $\ket{0}$ or $\ket{1}$, but at the same time its partner seems to know about this random choice and collapses into the same state. Because quantum mechanics suggests that this happens instantaneously, it seems to violate the premise of Einstein’s theory of relativity that information cannot travel faster than light.
This conclusion is not correct, though! To exploit the entangled state for information transmission, the sender would have to force the qubit to collapse either into $\ket{0}$ or $\ket{1}$, depending on the binary message “0” or “1” to transmit. But quantum mechanics does not allow measurement outcomes “to be forced”; they happen randomly with probabilities determined by the quantum state. So the randomness of the measurement outcome prevents us from using entangled qubit pairs to send information faster than the speed of light. This is not a consequence of our specific state but rather a general property of quantum mechanics known as the No-communication theorem. This means that quantum mechanics and Einstein’s special theory of relativity are perfectly consistent. Fully relativistic versions of quantum mechanics are used to describe models of high-energy physics like the Standard Model.
We discuss entanglement in our tutorial on the basics of quantum mechanics.
Ⓒ2023 Tutorial by Nicolai Lang, Institute for Theoretical Physics III, University of Stuttgart