Schrödinger’s cat

Quantum mechanics governs the world of the very tiny (single atoms and photons) and the very cold (like superconductors). These, however, are observations; the framework of quantum mechanics, detailed in our tutorial, does neither mention the very tiny nor the very cold. Quantum mechanics is silent about where exactly its dominion ends and transitions into the macroscopic world of classical physics. This was also realized by Erwin Schrödinger who cooked up the following vicious Rube Goldberg machine:

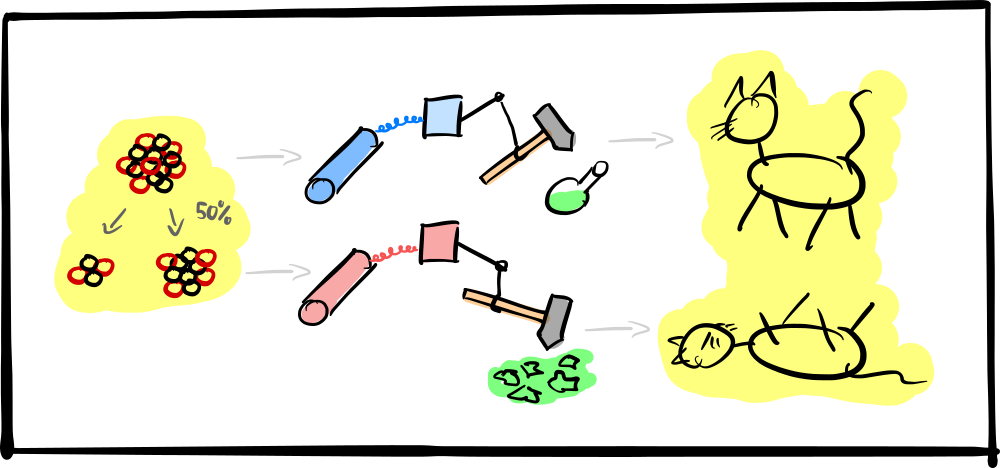
1. We prepare the experiment by placing a single radioactive nucleus, an apparatus, and a (living) cat in a box. The apparatus consists of a Geiger counter that is triggered with certainty when the nucleus decays. The trigger signal activates a box with a motor that lets a hammer crush a glass vial filled with poison. So when the nucleus decays, the cat dies.
2. Now we seal the box so that no information about the state of the contraption can leak outside. Then we wait for the half-life period of the radioactive nucleus. (If the nucleus is cabon-11 you have to wait for roughly 20 minutes.)
3. Finally, we open the box and observe the outcome. In 50% of the cases we will find our original nucleus, a sealed glass vial, and a living cat. In the other 50% of the cases the nucleus decayed, triggered the contraption, and poisoned the cat.

What is the point? Clearly we could do this experiment and it would undoubtedly play out the way explained above. The point is that up until we open the box the nucleus evolves according to the rules of quantum mechanics. This means that it does not simply decay or not decay, it rather evolves into a superposition of both states at once. Only when we open the box, and thereby “measure” the system, its wave function collapses into one of the two possible outcomes:

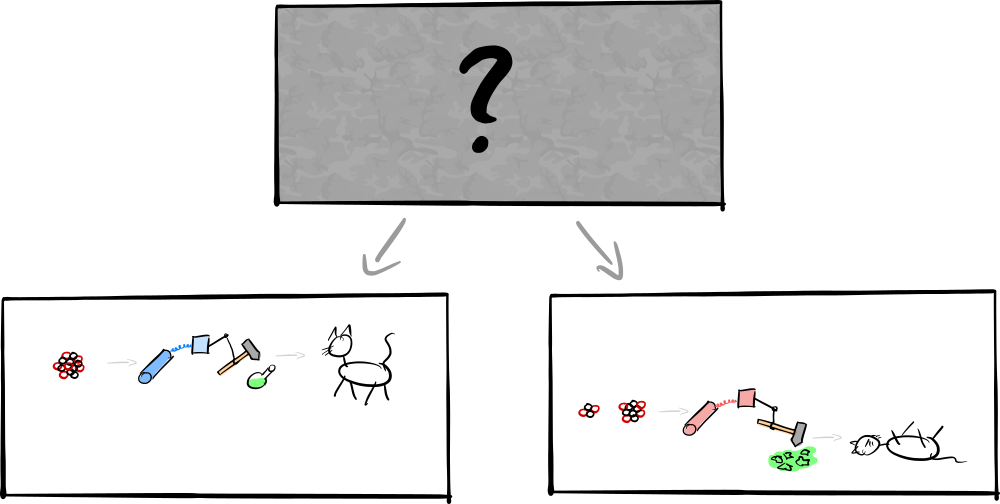
But we coupled the fate of the cat, via the contraption with the hammer and the glass vial, to the state of the nucleus! If one takes quantum mechanics seriously, and that’s the punchline of the experiment, then the cat becomes entangled with the nucleus and thereby “inherits” the superposition of the atom. The cat is in a superposition of being dead and alive up until we open the box and look!

To implement the experiment on our quantum computer simulator, we must cut corners. Since we as physicists are allowed to model cows as spheres, there shouldn’t be a problem with the assumption that our cat consists of 5 cells, one of which is it’s only brain cell (it’s a really tiny and really stupid cat!). Our cells are also very simple and have only two states: dead and alive. We assume that the cat is dead (alive) if all its cells are dead (alive). Let us label the state of the original nucleus as “0” and its decayed state as “1”. Similarly, a living cell is indicated by “0” and a dead one by “1”. Then the initial state of the combined system “nucleus-cat” is the 6-qubit state$$
\ket{\Psi_\mathrm{initial}}=\ket{0,00000}
$$ where we inserted a comma to separate the nucleus state from the five cell states. Note that this is just the quantum state that our quantum computer is initialized in when we setup the circuit simulator with 6 qubits. We interpret the state of q[0]as the state of the nucleus and the states of q[1]–q[5] as the states of the cells.

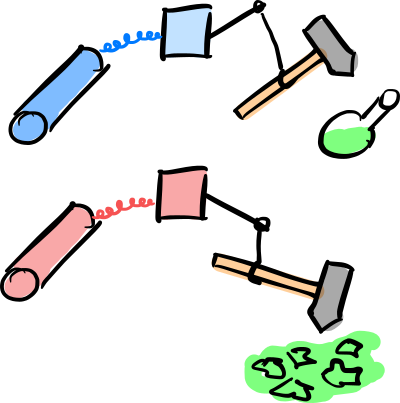
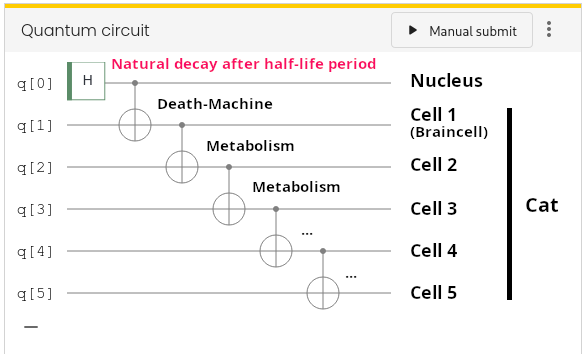
Next we must implement the apparatus. Of course we cannot model the full chain of a Geiger counter, motor, hammer, vial, and poison with our limited means. But we can implement an effective interaction by using a Controlled-NOT gate. Remember that a Controlled-NOT gate flips a target qubit only if the control qubit is in state $\ket{1}$. If we assume that the poison is a neurotoxin that kills brain cells, we can model the effect of a decayed nucleus on the single brain cell (modeled by qubit q[1]) by connecting the two qubits with a Controlled-NOT gate. We use the “nucleus qubit” q[0] as control and the “brain qubit” q[1] as target. Now q[1]is flipped from $\ket{0}$ (alive) to $\ket{1}$ (dead) if q[0] flips from $\ket{0}$ to $\ket{1}$ (= the nucleus decays). Furthermore, biology tells us that shortly after the brain dies, all other cells of the organism die as well. Let us model this “metabolic chain reaction” by a cascade of Controlled-NOT gates that sequentially trigger the death of cells, starting from the brain cell. The setup of (undecayed) nucleus, apparatus, and 5-cell cat then looks like this:

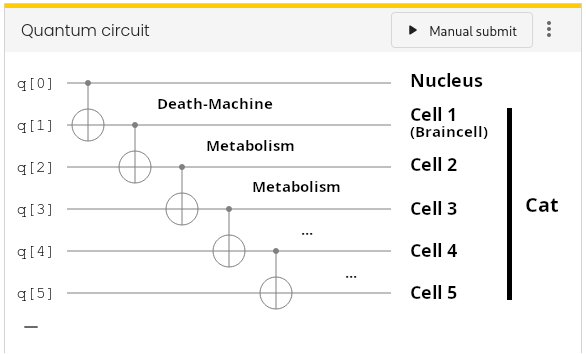
Run the circuit several times and observe the outcomes. The histogram tells you the probabilities for measurement outcomes at the end of the quantum circuit. In the thought experiment, this corresponds to the opening of the box at the end. Our model above should yield the measured state$$
\ket{\Psi_\mathrm{measured}}=\ket{0,00000}
$$ with certainty. In our interpretation this means that when opening the box we always find our original nucleus and a living cat. This shouldn’t surprise us. We forgot to make our nucleus decay! Look at the circuit: We initialize q[0] in the state $\ket{0}$ and then do nothing with it. So it stays in this state all along and consequently the cat never dies. Essentially we simulated a stable nucleus like helium-4. If we want the nucleus to decay, we must simulate this by changing its state with a gate.

Before we go full quantum, let us first make a (vicious) sanity check: Just before closing the box, we trigger a decay of the nucleus with certainty (by hitting and exciting it with a high energy neutron). In our model, we can represent this by the Pauli-X gate $X$ that acts on a single qubit and flips its state:$$
\begin{aligned}
\ket{0}\;&\xrightarrow{\;X\;}\;\ket{1}\\
\ket{1}\;&\xrightarrow{\;X\;}\;\ket{0}
\end{aligned}
$$In the circuit simulator, this gate is labeled by a box with the symbol $\oplus$. Grab this gate and squeeze it into the circuit right at the beginning on the q[0] “nucleus qubit”:

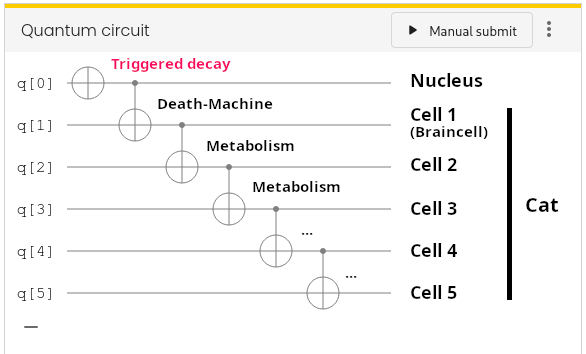
Run the circuit again several times. The observed state after opening the box should be now$$
\ket{\Psi_\mathrm{measured}}=\ket{1,11111}
$$ with certainty. Alas! The nucleus decayed (because we forced it to) and all cells of the cat are dead (and so is the cat). This result demonstrates that our “chain of death” build from Controlled-NOT gates works as expected: A decaying nucleus kills the cat, exactly what the original contraption envisioned by Schrödinger was supposed to do.

Now that we know that our setup works, let us finally simulate a real radioactive nucleus that quantum mechanically decays with probability 50% while we wait. After waiting for the half-life period, the “nucleus qubit” q[0] should end up in a superposition state of the form$$
\frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1}
$$so that the probability for a decay is $p_1=(1/\sqrt{2})^2=0.5$ if we observe the nucleus at the end. We already know that the single-qubit gate that creates this superposition from the initial state $\ket{0}$ (= not decayed) is the Hadamard gate $H$. We can therefore simulate the quantum evolution of the nucleus by inserting a Hadamard gate instead of the Pauli-X gate from above. To do this, pull the Pauli-X gate out of the Quantum circuit box to delete it and replace it by a Hadamard gate:

Run the simulation several times and study the histogram. You should observe the two states$$
\ket{\Psi_\mathrm{measured}}=\ket{0,00000}\quad\text{or}\quad\ket{\Psi_\mathrm{measured}}=\ket{1,11111}
$$with roughly the same probability of 50% (and no other outcome). In our interpretation, we find the two outcomes “nucleus not decayed & cat alive” and “nucleus decayed & cat dead” randomly with the same probability. This is exactly the outcome envisioned by Schrödinger! The quantum state in our simulator right before we measure (= open the box) is therefore$$
\ket{\Psi_\mathrm{final}}=\frac{1}{\sqrt{2}}\ket{0,00000}+\frac{1}{\sqrt{2}}\ket{1,11111}\,,
$$i.e. a superposition of a cat that is alive and dead at the same time (and an entangled nucleus that is not decayed and decayed at the same time). A state of this form is called a cat state for obvious reasons (sometimes the term GHZ state is used synonymously).

Note that above we were a bit sloppy: From the histogram produced by the simulator you cannot infer the relative sign of the second amplitude! (A negative amplitude $-1/\sqrt{2}$ would clearly result in the same probabilities.) However, you can check by hand that the above positive sign is indeed correct. While the relative sign is important in principle, it can be ignored for our present purpose to demonstrate the superposition of a “macroscopic” 5-cell cat that is both alive and dead at the same time.

What is the bottom line of our simulation? Would Schrödinger be shocked? Well, of course not! The result is exactly what he anticipated (more precisely: calculated, one does not need a simulator to find the cat state). His entire point was that if one takes quantum mechanics seriously, then a cat state must be the result of this experiment. So what is the problem? Is there a problem at all? Well, the situation is puzzling because we started to poke at the foundation of quantum mechanics (which we do not yet fully understand!). Let us try to clarify the situation with a few comments in Q&A style:

• If we would perform our 6-qubit experiment that we simulated above on a real quantum computer, what would be the outcome?
  The outcome would match our simulation perfectly. We know this because simple quantum circuits on a handful of qubits can already be implemented on existing quantum computer prototypes. They behave exactly as quantum mechanics predicts.
• If we would perform the original version of the thought experiment in reality, what would be the outcome?
  This is another experiment that we could in principle perform (though it might be ethically problematic). The result would be as anticipated: with 50% probability, the nucleus would have decayed and the cat died when we open the box. However, the cat would never be in a superposition of dead and alive. There are two immediate questions that pop up: How can we know without opening the box, and why is there no superposition? The answer to the first question is “interference”, the answer to the second one “decoherence”.
  Details coming soon.
• If we would perform an experiment similar to our simulation on a real quantum computer, where now the cat is represented by $\sim 10^{18}$ qubits (roughly the number of cells in a macroscopic organism), what would be the outcome?
  If quantum mechanics in its current form (as explained in our tutorial) is correct, it remains valid also for macroscopic systems. In particular, superpositions of the form$$
  \frac{1}{\sqrt{2}}|\underbrace{0\dots 0}_{10^{18}}\rangle+
  \frac{1}{\sqrt{2}}|\underbrace{1\dots 1}_{10^{18}}\rangle
  $$can be realized. However, because nobody succeeded in building a quantum computer with that many qubits so far (and will not in the foreseeable future), the honest answer is: We do not know. There are theories, known as objective-collapse theories, that reject the validity of quantum mechanics at such scales and posit a spontaneous or gravitationally induced collapse of the quantum state whenever one tries to superimpose macroscopic objects. So far we do not have experimental evidence of such collapse processes, but we also failed to superimpose macroscopic objects (most physicists blame decoherence for our failure and not objective collapse). To sum up: Whether one can really superimpose a cat in two states at once, given one has perfect control over decoherence, is one of the most profound unanswered questions of physics. Most physicists expect this to be possible in principle; but even a majority can err. Experiments are needed to settle this question.
• Why do we need the cat in the original formulation of the experiment? If the question is whether macroscopic objects can be in superpositions, or necessarily perform measurements and induce a collapse of the quantum state, wouldn’t the contraption with the hammer be sufficient?
  Yes, it would. The original formulation is multilayered and covers at least two different questions. The first is whether quantum mechanics applies to macroscopic objects. If it does, a hammer can be in two places at once. By contrast, if objective-collapse theories were correct, it cannot and forces the collapse of the quantum state. In this situation, the cat would never experience anything “quantum” and is irrelevant. So let us assume that the current formulation of quantum mechanics is correct and the hammer can be in two places at once. Now the cat becomes important as it must be in a superposition of dead and alive. This is the punchline, and everyone remembers it for a simple reason: a dead cat is unconscious, a living cat has probably some form of conscious experience like us. The cat now plays the role of an ethically acceptable proxy for us (conscious agents, that is). The formulation of the thought experiment coaxes us to put ourselves into the position of the cat and wonder how it “feels” to be dead and alive at the same time, or to see a hammer being in two places at once. This is a very different (and much deeper) question than whether an unconscious hammer can be in two places at once. It provokes the question whether consciousness plays any role in the quantum mechanical measurement process (a mindset that was quite common in the early days of quantum mechanics, but is dismissed by most physicists today). The problem has been sharpened later by Eugene Wigner with a related thought experiment, known as Wigner’s friend, where the cat is essentially replaced by a human observer. We are now up to our throat in a philosophical quagmire that many admirable thinkers got stuck in. So let us stop here with a reformulation of the issue that Schrödinger wanted to drive home with his famous thought experiment:
  
  Why do we experience a macroscopic world without quantum phenomena like superpositions? Which processes qualify as “measurements” in quantum mechanics? Equivalently, what triggers the collapse of quantum states? Macroscopic objects, “the environment”, or conscious agents? Is there a collapse to begin with? Where is the border between the microscopic quantum world and the macroscopic classical world? Does this border exist at all?
  
  There is no consensus among physicists how to answer these questions (there is not even consensus whether they are the right questions to ask!). To sum up all this confusion, physicist coined a new term: The measurement problem. It is one of these problems that are hard to grasp because already their formulation is fuzzy. It is also one of the most fundamental problems of modern physics and might very well be linked to another fundamental problem, namely the formulation of a consistent theory of quantum gravity.